7. díl - Výpočet obsahu křivky v X-Y zobrazení

Mnoho aplikací zahrnujících cyklické jevy vede k potřebě určit oblast ohraničenou křivkou v zobrazení X-Y.

Technický seriál - Rady a tipy při výběru osciloskopu

Autor Bohumil Vítovec 

Mnoho aplikací zahrnujících cyklické jevy vede k potřebě určit oblast ohraničenou křivkou v zobrazení X-Y. 

Typickým příkladem je ztráta energie na cyklus v magnetickém jádru, která je úměrná ploše uzavřené grafem intenzity magnetického pole proti hustotě toku. Tuto oblast lze snadno automaticky měřit pomocí matematických funkcí dostupných v osciloskopech Teledyne LeCroy.

Plochu uzavřenou v grafu XY lze vypočítat jako:

Osciloskop má data pro obě stopy jako funkci času, t. Proměnné lze změnit v integrálu a vypočítat plochu na základě získaných stop.

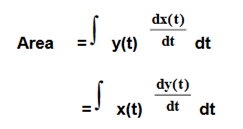
Abychom tento postup mohli implementovat v osciloskopu, musíme diferencovat jednu ze stop, pak ji vynásobit druhou stopou a integrovat výsledek.

Integrál, vyhodnocený v průběhu 1 cyklu periodického průběhu, se rovná ploše obsažené v grafu X-Y.

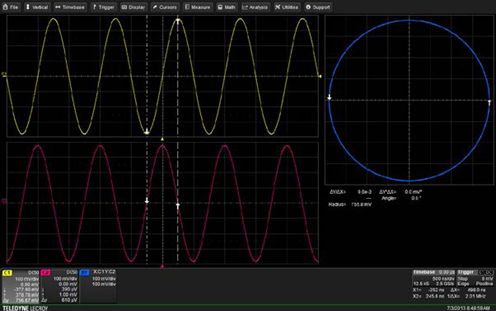
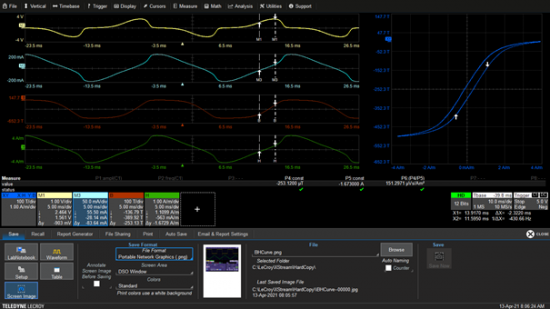
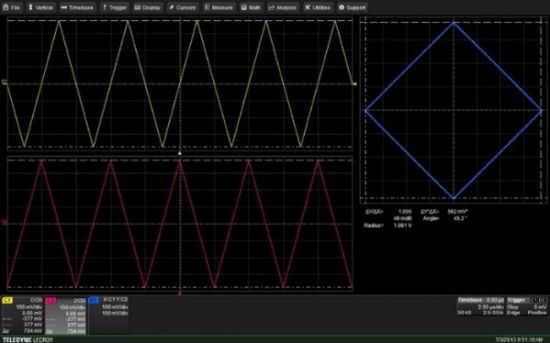
Obrázek 1: obsah kruhu=Pi (0.7558/2)^2=0.4486 V^2

Obrázek 1 ukazuje graf X-Y obklopující kruhovou oblast. Na základě geometrie displeje měřené pomocí kurzorů X-Y můžeme určit uzavřenou oblast jako test výše popsaného procesu. Kurzory relativní amplitudy měří průměr kruhu jako 756 mV.

Na obrázku 2 je skutečný výpočet proveden s velmi shodnými výsledky. Plošný parametr křivky produktu (F2) ve stejné oblasti (jeden cyklus vstupní křivky) vytváří stejný výsledek.

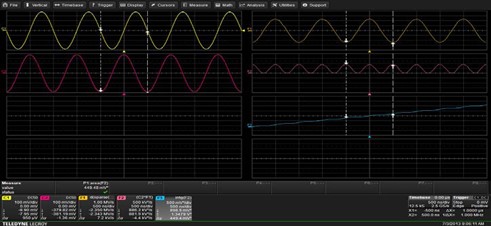
Obrázek 2: Vypočtený obsah =0.449 V^2​

Několik rad pro maximalizaci přesnosti:​

Aby se minimalizoval šum, měla by se derivace počítat s minimálním počtem bodů. V následujících příkladech byly matematické operace provedeny s použitím 500 bodů.

Maximalizujte vstupní signály v dynamickém rozsahu pomocí variabilního útlumu. Obrázky 3 a 4 obsahují další příklad využívající snadno ověřitelnou postavu, čtverec. Geometrická plocha se stanoví pomocí odečtů kurzoru X-Y jako 0,284 V2. Výpočet plochy vede k výsledku 0,285 V2, jak je čteno z pole ukazatele kurzoru pro matematickou stopu F3 (integrál).

 Obrázek 3

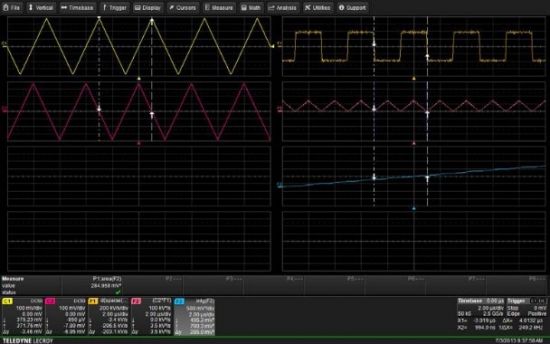
Obrázek 4

Osciloskopy Teledyne LeCroy nabízejí vysokou úroveň funkční integrace, která je v této aplikaci evidentní. Nastavení displeje X-Y zahrnují kartézské i polární souřadnicové kurzory, což usnadňuje referenční měření. Matematické funkce lze zřetězit, což umožňuje až 16 simultánních matematických operací (v závislosti na modelu) najednou.

V tomto seriálu si neklademe za cíl hodnotit, která značka je nebo není nejlepší. Chceme pouze čtenáře upozornit na častá omezení a úskalí, která nemusí být na první pohled při výběru osciloskopu pro vaší práci zřejmá. Chceme vám poskytnout určitý nadhled při výběru nového osciloskopu. Informace, které v seriálu uvádíme, vychází z našich dlouholetých zkušeností s osciloskopy a především s přístroji Teledyne LeCroy, z veřejně dostupných informací a technické dokumentace ostatních výrobců. Abychom se nezabývali touto problematikou jen v teoretické rovině, zaměříme se na technické parametry přístrojů a různé způsoby měření. 

Obsah tohoto seriálu můžete také ovlivnit! Uvítáme vaše komentáře, návrhy témat, vaše zkušenosti, které můžete zasílat na email bohumil.vitovec@blue-panther.cz.

Stejně tak se můžete ozvat, pokud potřebujete radu na míru!

Další díl / Všechny díly