4. díl - Spektrální analýza, Fourierova transformace

Moderní digitální osciloskopy umožňují provádět s naměřenými daty v reálném čase nejrůznější jednoduché i složitější matematické operace. Mezi náročnější matematické operace bezesporu patří Fourierova transformace, přepočet průběhu signálu z časové do frekvenční domény, tedy spektrální analýza. V tomto díle našeho technického seriálu se zaměříme právě na spektrální analýzu.

Technický seriál - Rady a tipy při výběru osciloskopu

Autor Bohumil Vítovec

Osciloskop je přístroj určený primárně pro zobrazení úrovně signálu v závislosti na času. Moderní digitální osciloskopy umožňují provádět s naměřenými daty v reálném čase nejrůznější jednoduché i složitější matematické operace. Mezi náročnější matematické operace bezesporu patří Fourierova transformace, přepočet průběhu signálu z časové do frekvenční domény, tedy spektrální analýza. Fourierova transformace (dále uváděna jako FT) je integrální transformace převádějící signál mezi časově a frekvenčně závislým vyjádřením, pomocí harmonických signálů, funkcí sin a cos. Obecně tedy funkcí komplexní exponenciály. Def [3]

Fourierova transformace slouží pro převod signálů z časové oblasti do oblasti frekvenční. Signál může být buď ve spojitém či diskrétním čase. Pro diskrétní časová data se výpočetní algoritmus nazývá diskrétní Fourierova transformace (DFT) a vyžaduje N2 komplexních součinů a součtů. Za jistých podmínek lze uplatnit mnohem rychlejší algoritmus, rychlou Fourierovu transformaci (dále uváděna jako FFT). Pro FFT neboli rychlou Fourierovu transformaci stačí N log2 N komplexních součinů a součtů. Tato funkce ve výsledku poskytuje alternativní náhled na měřená data. Díky FFT můžeme změřit z jakých frekvenčních složek se náš signál skládá.

Před tím, než provedete měření nebo budete analyzovat signál, doporučujeme vám se zamyslete nad tím, co od měření očekáváte a uvědomte si stav a omezení nastavení vašeho měření analyzujte výsledky:

• Jak je nastavená napěťová a časová základna;
• Vertikální rozlišení a horizontální rozlišení;
• Rozsah šířky pásma;
• Impedanční přizpůsobení;
• Jaké mají tyto nastavení vliv na výpočet FFT;
• Jsou výsledky měření v souladu s tím, co jste očekával?
• Co uděláte se získanými informacemi z měření?

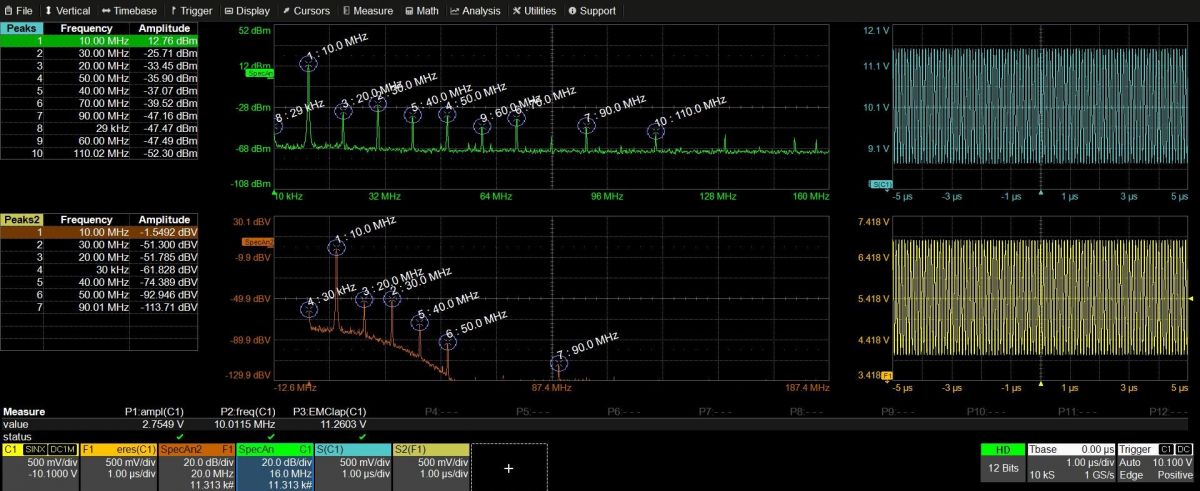
Obrázek č. 1: Příklad duálního spektrálního analyzátoru na osciloskopu Teledyne LeCroy Wavepro HD 12b 2.5GHz

Na obrázku č.2 uvidíte konkrétní příklad:

Amplitudová modulace signálu AM vzniká tak, že sinusový signál o frekvenci f0 zesilujeme a zeslabujeme, zde například jednoduchým sinusovým signálem o frekvenci f1.

n(t)= N sin(2Pi f0 t) Popis nosného signálu

m(t)=M sin(2Pi f1 t) Popis modulace

y(t)=(N+M sin(2 Pi f1 t))sin (2Pi f0 t) Modulovaný signál získáme vynásobením m(t)*n(t)

y(t)=N sin(2 Pi f0 t) +0.5Mcos((2Pif0-2Pif1)t)-0.5Mcos((2Pif0+2Pif1)t)

Měli bychom tedy očekávat, že uvidíme na osciloskopu ve spektrální oblasti signál nosné frekvence a dva slabší signály rozdílových frekvencí:

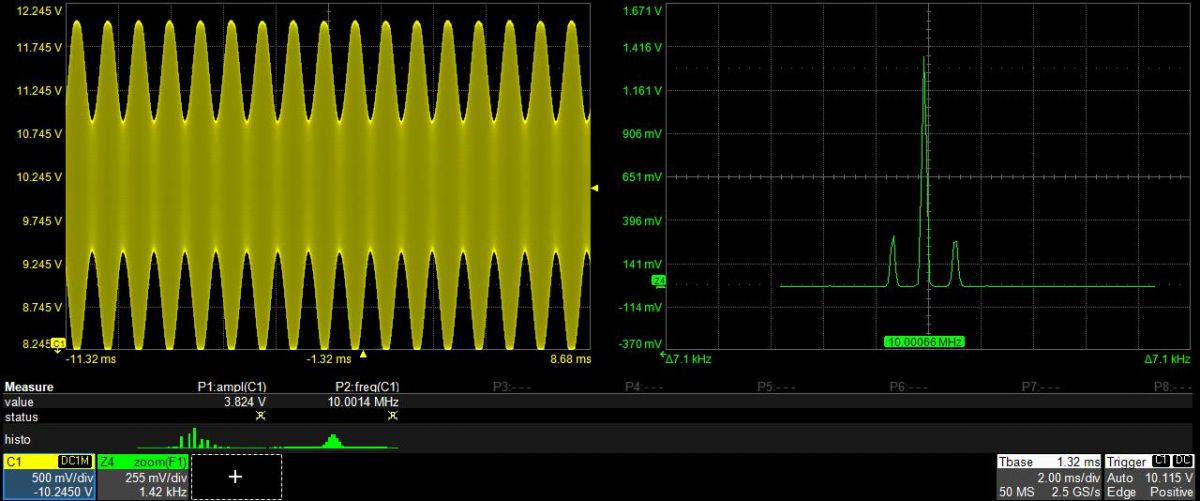
Obrázek č.2: Jednoduchá AM modulace sinusového signálu (vlevo) , vpravo je vidět frekvenční složky modulovaného signálu. (generátor amplitudově modulovaného signálu GenTrad, osciloskop Teledyne LeCroy HDO6054)

Základní předpoklady fungování spektrální analýzy na digitálních osciloskopech [1]:

• Diskrétní Fourierova transformace (DFT) je implementována jako FFT;
• Signál se opakuje, opakovaná perioda je v akvizičním okně;
• Pro FFT, se používá 2n bodů z časové domény (použití zaokrouhlovacího okna);
• První harmonická spektra je k x1/(délka akvizice);
• Nejnižší frekvence =1st harmonická (časová základna okna);
• f0=1/T0 (T0 celková doba akvizičního okna);
• Nejvyšší frekvence je ½ (samplovací rychlosti);

Příklad převodu měřítka z časové oblasti do frekvenční:

Akviziční okno: 10 ms → rozlišení je 1/0.01 s=100 Hz

Samplovací rychlost: 250 MS/s → Maximální frekvence je ½ x 250 MS/s= 125 MHz
 

Osciloskopy Teledyne LeCroy vás dokáží těmito nastaveními přehledně a rychle provést. Díky dostatečnému výpočetnímu výkonu nedojde ke zpomalení měření analogového signálu. Navíc lze na výsledky Fourierovy transformace použít veškeré výpočetní a analytické nástroje softwarového vybavení osciloskopu viz Obrázek č.2. Dále je k dispozici jak samotná FFT signálu možnost grafického zobrazení FFT ve formě jakou disponují standardní spektrální analyzátory, včetně vyhledávání píků, jejich označení a zobrazení v tabulce. U středních a vyšších řad osciloskopů Teledyne LeCroy lze zobrazení spektrálního analyzátoru použít na dva různé signály najednou viz. Obrázek č.1.

Pokud Vás tento krátký článek zaujal, doporučuji zhlédnout webinář od Teledyne LeCroy, kde se dozvíte podrobnější funkce nastavení FFT na osciloskopech LeCroy [1].

[1] Faster Time to Insight Using Real Time Spectral Analysis of Power Rails

https://go.teledynelecroy.com/l/48392/2018-04-10/6pqp51 [cit:02.11. 2018]

[2]Analýza signálů ve frekvenční oblasti

https://www.kiv.zcu.cz/~mautner/Azs/Azs5_Fourierova_transformace.pdf [cit:26.09.2018]

[3]Fourierova transformace

https://cs.wikipedia.org/wiki/Fourierova_transformace [cit:26.09.2018]

V tomto seriálu si neklademe za cíl hodnotit, která značka je nebo není nejlepší. Chceme pouze čtenáře upozornit na častá omezení a úskalí, která nemusí být na první pohled při výběru osciloskopu pro vaší práci zřejmá. Chceme vám poskytnout určitý nadhled při výběru nového osciloskopu. Informace, které v seriálu uvádíme, vychází z našich dlouholetých zkušeností s osciloskopy a především s přístroji Teledyne LeCroy, z veřejně dostupných informací a technické dokumentace ostatních výrobců. Abychom se nezabývali touto problematikou jen v teoretické rovině, zaměříme se na technické parametry přístrojů a různé způsoby měření. 

Obsah tohoto seriálu můžete také ovlivnit! Uvítáme vaše komentáře, návrhy témat, vaše zkušenosti, které můžete zasílat na email bohumil.vitovec@blue-panther.cz.

Stejně tak se můžete ozvat, pokud potřebujete radu na míru!

Další díl / Všechny díly